

4.4. Wave Behaviour
Now we look in a bit of detail about some of the cool behaviours of waves. You will have looked at reflection and refraction before, and perhaps diffraction. Light waves are able to reflect and refract, though in fact all of these behaviours (reflection, refraction, diffraction) are properties shared by all waves. Over the centuries, great scientists have debated extensively about whether light is a wave (as believed by Maxwell, Hooke, Huygens) or a particle (Newton, Einstein). This chapter introduces something called the Young's Double Slit experiment - although very simple, it is a hugely important demonstration of the wavelike nature of light.
Crash Course have a nice little introduction to these ideas.
This section has been divided up as follows:
-
Reflection and Refraction - what happens when a wave encounters a different medium?
-
Snell's Law and TIR - diving into the mathematics behind refraction
-
Diffraction - waves spreading out when they encounter a gap or barrier
-
Double Slit Interference - a brief introduction to this important experiment
Reflection and Refraction
You should have encountered the basic ideas of reflection and refraction at GCSE, and have probably had a go at some experiments to visualise these effects.
You should be familiar with the law of reflection - the angle of incidence is always equal to the angle of reflection. The key thing to remember here is that the angles are always measured relative to the normal.

One of the classic Physics experiments that almost everyone tries in class is using a glass block to calculate the refractive index of the material. The video below explains the key steps of this practical.
Why does refraction occur in the first place? This gif shows wave fronts being emitted from a point source. When these wave fronts hit the boundary of a new medium, they slow down, causing the wave fronts to get closer together (the wavelength decreases). This slowing down may also cause the waves to change direction if they are incident to the boundary surface at an angle.
If we look at our wave equation:
Wave speed (msˉ¹) = Frequency (Hz) x Wavelength (m)
v=fλ
The wave speed decrease in the new medium, as does the wavelength (by the same proportion). This means that the wave frequency in each medium remains the same.

There are a few analogies that we use to explain why we get this change in wave direction when entering a new medium. The car driving through mud helps us predict which way our ray will bend in the new medium. To really understand these behaviours, it's useful to understand a little about the Huygens Construction of waves - a new way of thinking about wave behaviour devised by Dutch physicist Christiaan Huygens - one of the key proponents on the wave-like nature of light. Isaac Physics have some lessons on this.
Walter Fendt has a couple of really informative simulations to check out.
-
First we have a simple illustration of refraction and refraction occurring at a boundary between two media and how the angles vary with refractive index.
-
The second explains the phenomena of reflection and refraction using something called Huygens' Principle. Although this is beyond the IB curriculum, there's some really nice Physics at play here.
Video Lessons
Chris Doner | Reflection and Transmission | IB Specific | ||||
Khan Academy | Specular and Diffuse Reflection | Specular and Diffuse Reflection 2 | Refraction in Water | |||
Physics Online | Introduction | EM Wavespeed and RI | Refraction Explained Further | |||
Science Shorts | Refraction & TIR | |||||
Study Nova | Reflection & Refraction | Reflection & Refraction (Lecture) |
Resources
IB Physics | Topic 4 Notes | |||||
IB-Physics.net | Chapter 4 Summary | IB Revision Notes | ||||
Isaac Physics | Reflection and Refraction | Ray Diagrams Recap | ||||
Mr. G | 4.4 Teaching Notes | 4.4 Student Notes | ||||
Physics and Maths Tutor | Waves Definitions | Waves Key Points | Waves Detailed Notes | Waves: Diffraction, Refraction, Interference | A Level Resources - content slightly different |
Questions
Cambridge University Press | Topic 4: Add Qs | Topic 4: Add Qs MS | Topic 4: MCQs | CUP Website Link | Freely available online | |
Grade Gorilla | 4.4 (Refraction) MCQ | Topic 4 (Waves B) End Quiz | Quick IB Specific Mixed MCQs | |||
Isaac Physics | Refraction and TIR | Mixed Questions | ||||
Mr. G | 4.4 Formative Assessment | Topic 4 Summary Qs | IB Specific Questions | |||
Physics and Maths Tutor | Refraction (AQA 1) | Refraction MS (AQA 1) | Refraction (AQA 2) | Refraction MS (AQA 2) | A-Level Qs: overlapping content | |
Physics and Maths Tutor | MCQ Refraction, Diffraction, Interference (AQA 2) | MCQ Refraction, Diffraction, Interference MS (AQA 2) | A-Level Qs: overlapping content |
Snell's Law and Total Internal Reflection
Refractive Index
The refractive index is a measure of how much light (or other waves) slow down in different media. It is given by the following equation.


The refractive index is characteristic of the material. A vacuum has a refractive index of 1, with air having a value very close to 1 (normally approximated as 1). The slower that light travels in the material, the higher the refractive index.
Snell's Law
Snell's law describes mathematically the angle through which light bends when moving from one medium to another. It's worth drawing a ray diagram to accompany when using Snell's Law, as shown below. The ray moves from a material with refractive index n1 to a medium with refractive index n2. The angles of incident and refracted angles are θ1 and θ2 respectively.
-
If n1 < n2 (less dense medium to more dense, e.g. air to water) : The ray bends towards the normal (as below).
-
If n1 > n2 (more dense medium to less dense, e.g. air to water) : The ray bends away from the normal.
-
If n1 = n2 (same refractive index) : The ray will not change direction.

PHET have a simulation that allows you visualise these main ideas to do with refraction, and to take some measurements to calculate refractive index. You can also investigate dispersion through prisms of different geometries.
Total Internal Reflection
The below diagram shows light moving from a medium with a high refractive index to a lower refractive index (e.g. from glass to air).
-
Picture 1 shows the ray bending away from the normal in the new material. As we increase the angle of incidence, the refracted angle gets larger, with the emerging ray bending closer and closer to the boundary between the two materials.
-
There is a point where the refracted ray runs right along the material boundary (i.e. θr = 90°): the angle of incidence at this point is called the CRITICAL ANGLE.
-
Any incident angles greater than this critical angle will not emerge from the block, instead they will be reflected back inside. This is called TOTAL INTERNAL REFLECTION.
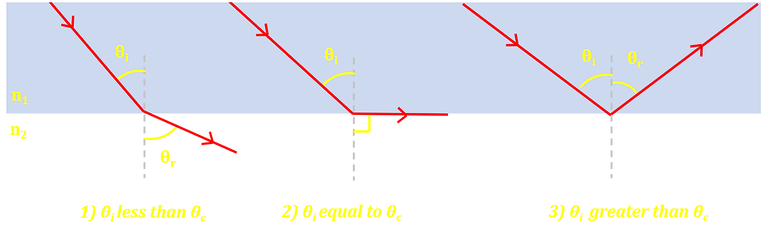
The exact value of this critical angle depends on the two media through which the ray travels. We can use Snell's law to work this out mathematically. If we substitute in θc (critical angle) for θi , and 90° for θr, we can work out a mathematical expression for our critical angle.

In the situation when light moves from a denser medium to air (n=1) (e.g. from water to air), this equation becomes:

Required Practical - Calculating refractive index
Another required practical - calculating refractive index using a glass block. The below video explains how we can do this using a semi-circular glass prism and these ideas about total internal reflection.
Video Lessons
Chris Doner | Snell's Law of Refraction | IB Specific | ||||
Khan Academy | Refraction and Snell's Law | Total Internal Reflection | Snell's Law Example 1 | Snell's Law Example 2 | ||
Physics Online | Refraction and Snell's Law | TIR and Critical Angle | ||||
Science Shorts | Refraction & TIR | |||||
Study Nova | Reflection & Refraction |
Resources
IB Physics | Topic 4 Notes | |||||
IB-Physics.net | Chapter 4 Summary | IB Revision Notes | ||||
Mr. G | 4.4 Teaching Notes | 4.4 Student Notes | ||||
Physics and Maths Tutor | Waves Definitions | Waves Key Points | Waves Detailed Notes | Waves: Diffraction, Refraction, Interference | A Level Resources - content slightly different |
Questions
Cambridge University Press | Topic 4: Add Qs | Topic 4: Add Qs MS | Topic 4: MCQs | CUP Website Link | Freely available online | |
Grade Gorilla | 4.4 (Refraction) MCQ | Topic 4 (Waves B) End Quiz | Quick IB Specific Mixed MCQs | |||
Isaac Physics | Refraction and TIR | Mixed Questions | ||||
Mr. G | 4.4 Formative Assessment | Topic 4 Summary Qs | IB Specific Questions | |||
Physics and Maths Tutor | Refraction (AQA 1) | Refraction MS (AQA 1) | Refraction (AQA 2) | Refraction MS (AQA 2) | A-Level Qs: overlapping content | |
Physics and Maths Tutor | MCQ Refraction, Diffraction, Interference (AQA 2) | MCQ Refraction, Diffraction, Interference MS (AQA 2) | A-Level Qs: overlapping content |
Diffraction
Diffraction is touched upon in GCSE, but without going into much depth. When waves encounter obstacles (e.g. barriers, slits, edges of objects), they are able to bend around them - this is called DIFFRACTION. Now, there are a few important experiments we will study that are a direct result of a wave diffracting.
The amount of diffraction occurring is greatest when the obstacle (the barrier or slit width) has a width of a similar order of magnitude to the waves.
Falstad have an excellent simulation of a ripple tank. that we looked at in the previous section.
From the drop down menu, select the following and observe the wave diffraction in each case.
-
Single Slit
-
Obstacle
-
Half Plane
Video Lessons
Chris Doner | Diffraction | IB Specific | ||||
Study Nova | Diffraction | Diffraction (Lecture) |
Resources
IB Physics | Topic 4 Notes | |||||
IB-Physics.net | Chapter 4 Summary | IB Revision Notes | ||||
Isaac Physics | Diffraction | Level 6 Beyond IB | ||||
Mr. G | 4.4 Teaching Notes | 4.4 Student Notes | ||||
Physics and Maths Tutor | Waves Definitions | Waves Key Points | Waves Detailed Notes | Waves: Diffraction, Refraction, Interference | A Level Resources - content slightly different |
Questions
Cambridge University Press | Topic 4: Add Qs | Topic 4: Add Qs MS | Topic 4: MCQs | CUP Website Link | Freely available online | |
Grade Gorilla | Topic 4 (Waves B) End Quiz | Quick IB Specific Mixed MCQs | ||||
Mr. G | 4.4 Formative Assessment | Topic 4 Summary Qs | IB Specific Questions | |||
Physics and Maths Tutor | MCQ Refraction, Diffraction, Interference (AQA 2) | MCQ Refraction, Diffraction, Interference MS (AQA 2) | A-Level Qs: overlapping content | |||
Physics and Maths Tutor | Diffraction Q | Diffraction MS | A-Level Questions (not all relevant) | |||
Physics and Maths Tutor | Diffraction (AQA 1) | Diffraction MS (AQA 1) | Diffraction (AQA 2) | Diffraction MS (AQA 2) | A-Level Qs: overlapping content |
Double Slit Interference
Diffraction is a wave characteristic, similar to interference that we saw in the previous section.
In the era of classical Physics, there was some debate about whether light was a particle or a wave. Newton was a big proponent of the particle-nature of light, believing it was made of many tiny light particles called corpuscles. Proponents of the wave-like nature of light included Huygens. In reality, light behaves very weirdly and exhibits behaviour of both particles and waves, which will be explored later.
As far as evidence of light's wave-like nature, there is a particularly important experiment, called Young's Double Slit Experiment, that uses the ideas of interference and diffraction to demonstrate the wave-like nature of light which will be explored here.
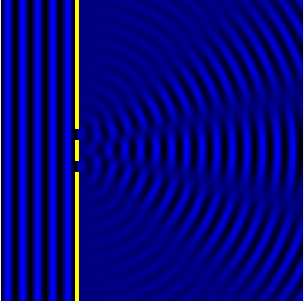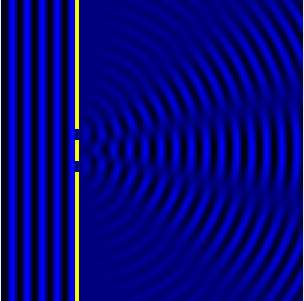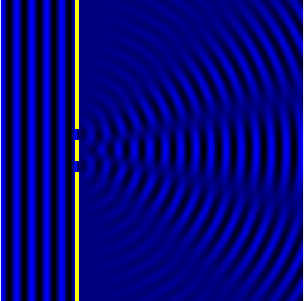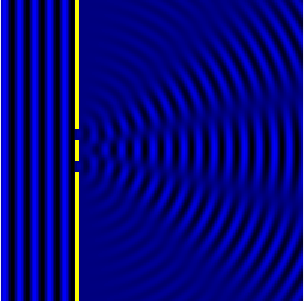
The setup for Young's Double Slit is shown below (with laser light instead of an electron beam.
-
Light from the laser beam hit the two slits and emerges on the other side. Light from each slit is coherent - that means it is in phase and of the same wavelength/ frequency.
-
Light from each of these slits interferes with light from the other slit, creating an interference pattern on the back screen.
-
The interference pattern is made up of bright fringes (of constructive interference from each slit) and dark fringes (of destructive interference from each slit)

Path Difference
Key to understanding the reason behind the formation of this interference pattern is the idea of path difference. Light from one slit travels a different distance to get to the back screen than light from the other slit. It is the difference in distance travelled from each slit, or path difference, that leads to corresponding bright and dark fringes.
-
When the path difference is an integer multiple of the wavelength (i.e. = nλ, where n is an integer), the light from each slit will arrive at the back screen IN PHASE, therefore will CONSTRUCTIVELY INTERFERE, resulting in a BRIGHT FRINGE.
-
When the path difference is a half-integer multiple of the wavelength (e.g. = 0.5, 1.5, 2.5 λ ...), the light from each slit will arrive at the back screen IN ANTIPHASE, therefore will DESTRUCTIVELY INTERFERE, resulting in a DARK FRINGE.
This Geogebra simulation exhibits more clearly this idea of path difference. Use a larger wavelength to make things more visible and move the blue slider on the right. You can see when the two waves arrive in phase or in antiphase, and how this causes bright and dark fringes respectively.
Double Slit Equation
We have an equation that describes the fringe separation of the resulting interference pattern. The derivation is fairly straightforward, Isaac Physics go through it here. (Note: This equation makes use of the smal angle approximation, i.e. is assuming that D >> d).

Another simple but clear simulation from Walter Fendt here - this allows you to play around with each variable and to look at the effect on the interference pattern.
Video Lessons
Chris Doner | Double Slit Experiment | 2 Source Interference | IB Specific | |||
Khan Academy | YDS Introduction | YDS Equation | YDS Problems | |||
Physics Online | Two Source Interference | Young's Double Slit | Practical Tips | |||
Science Shorts | Young's Double Slit | Practical Tips | ||||
Study Nova | Slit Diffraction |
Resources
IB Physics | Topic 4 Notes | |||||
IB-Physics.net | Chapter 4 Summary | IB Revision Notes | ||||
Isaac Physics | Young's Double Slits | Level 6 Beyond IB | ||||
Mr. G | 4.4 Teaching Notes | 4.4 Student Notes | ||||
Physics and Maths Tutor | Waves Definitions | Waves Key Points | Waves Detailed Notes | Waves: Diffraction, Refraction, Interference | A Level Resources - content slightly different |
Questions
Cambridge University Press | Topic 4: Add Qs | Topic 4: Add Qs MS | Topic 4: MCQs | CUP Website Link | Freely available online | |
Grade Gorilla | 4.3/4 (Interference) MCQ | Topic 4 (Waves B) End Quiz | Quick IB Specific Mixed MCQs | |||
Isaac Physics | Path Difference | Mixed Questions | ||||
Mr. G | 4.4 Formative Assessment | Topic 4 Summary Qs | IB Specific Questions | |||
Physics and Maths Tutor | Interference (AQA 2) | Interference MS (AQA 2) | A-Level Qs: overlapping content |
Additional Resources
IB Questions
A question by question breakdown of the IB papers by year is shown below to allow you to filter questions by topic. Hopefully you have access to many of these papers through your school system. If available, there may be some links to online sources of questions, though please be patient if the links are broken! (DrR: If you do find some broken links, please contact me through the site)
Questions on this topic (Section 4) are shown in light blue.
Use this grid to practice past IB questions topic by topic. You can see from the colours how similar the question topic breakdown is year by year. The more you can familiarise yourself with the IB question style the better - eventually you will come to spot those tricks and types of questions that reappear each year.









