
7.3. The Structure of Matter
This section firstly discusses a famous experiment which lead to the 'solar system' or Rutherford model of the atom which we are familiar with from GCSE - the gold foil scattering experiment.
The second half of this section is a whistle-stop tour of the Standard Model - a model which contains all known subatomic particles and antiparticles. There is a LOT here - introducing the idea of antimatter, as well as exotic particles such as pions and neutrinos.
Finally we touch on the idea of the 4 fundamental forces of the universe and their respective exchange particles. These are graphically represented using Feynman diagrams named after every physicists hero, Richard Feynman.
Before we get started, a nice little introduction from TedEd answering the question, 'What is the smallest thing in the universe?'
The section has been divided up as follows:
-
Rutherford Scattering - a key experiment in coming up with the current model of the atom
-
The Standard Model - a collection of all the subatomic particles we currently know of
-
Fundamental Forces - the 4 forces that make up the universe
-
Feynman Diagrams - a graphical representation of different particle interactions
Rutherford Scattering
Prior to early 20th century, physicists had discovered the existence of charge within the atom (since JJ Thompsons discovery of the electron in 1897). At the time, common wisdom amongst physicists was that the atom was like a 'plum pudding', (or blueberry muffin for the modern equivalent) - with a positively charged 'dough' studded with negatively charged 'plums'. One of the most famous experiments of 20th century was the Geiger Marsden experiment (or Rutherford gold foil experiment). This experiment provided evidence disproving the Plum Pudding model of the atom and laid the groundwork for the modern model of the atom as we know it.
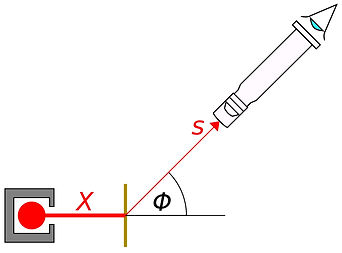
The experimental setup involves an alpha source pointing at a single sheet of very thin gold foil. An alpha detector is placed at positions around the gold foil which flashes when an alpha particle strikes it. The angle of this detector can be rotated 360° to determine the angle of deflection of the alpha particles as they pass through the foil. The diagram on the right below demonstrates this idea - the angle of deflection, Φ, is a result of the electrostatic repulsion between the positive alpha particles and the small, positively charged nucleus. To see a modern version of this setup, take a little look at the video below:
The results of the Geiger Marsden experiment were very unexpected. The plum pudding model (Thomson model below) predicted that most of the alpha particles should pass straight through through the foil - a low charge density in the 'dough' would not result in significant deflections. However, there were three key observations that led to the model of the atom as we know it:
-
Most of the alpha particles passed straight through undeflected (99%) - suggesting that most of the atom was made up of empty space.
-
Some of the alpha particles were deflected by small angles - suggesting that there was a small region within the atom of the same charge as the alpha particles (i.e. positive).
-
A small fraction (1 in 20 000) of the alpha particles were deflected through very large angles (up to 180°) - suggesting this positively charged region was very small with a high charge density
This led to the model of the atom as containing a very small positively charged nucleus within the centre of the atom. We now know this as the nucleus. We can compare what the 'plum pudding model' predicted vs the actual results in the diagram below. It is important to note that this experiment did not tell us of the existence of the neutron - because these have no charge they are much harder to detect. The electrons being in orbit around the nucleus and having a relatively tiny mass are unlikely to cause any significant deflections to the much more massive alpha particle (think throwing a ping pong ball at a truck).
It's worth here just reminding us about some relative sizes (you DO need to know these values) - an atom has an approximate diameter of 10ˉ¹⁰ m, while a nucleus has a diameter of approximately 10ˉ¹⁵ m (i.e. 100 000 times smaller).
PHET have another nice simulation where you can compare the results for the Rutherford atom and the Plum Pudding atom.
Predict what will happen in the following circumstances and see if you are correct:
-
increasing the energy of the alpha particles
-
increasing the proton number of the nucleus
-
increasing the neutron number of the nucleus
The key points of this experiment are explained nicely below by Tyler DeWitt .
Video Lessons
Chris Doner | The Atom (Rutherford Scattering) | IB Specific | ||||
Khan Academy | Gold Foil Experiment | |||||
Science Shorts | Alpha Scattering |
Resources
IB Physics | Topic 7 Notes | |||||
IB-Physics.net | Chapter 7 Summary | IB Revision Notes | ||||
Mr. G | 7.3 Teaching Notes | 7.3 Student Notes | ||||
Physics and Maths Tutor | Particles Definitions | Particles Key Points | Particles Detailed Notes | Particles Flashcards | A Level Resources - content slightly different |
Questions
Cambridge University Press | Topic 7: Add Qs | Topic 7: Add Qs MS | Topic 7: MCQs | CUP Website Link | Freely available online | |
Grade Gorilla | 7.2 (Particles) MCQ | Topic 7 (Nuclear) End Quiz | Quick IB Specific Mixed MCQs | |||
Mr. G | 7.3 Formative Assessment | Topic 7 Summary Qs | IB Specific Questions |
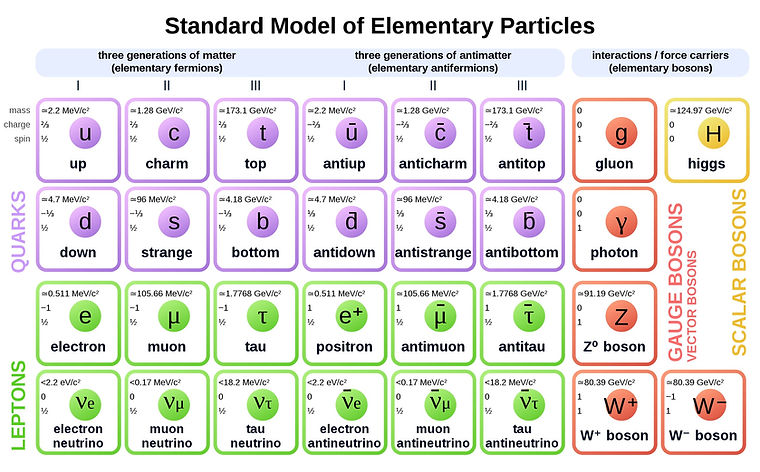
The Standard Model
We have discussed a number of subatomic particles so far - the proton, neutron and electron. These are just a small selection of the entirety of subatomic particles we are aware of. Through particle colliders (such as the one in CERN), we have discovered a whole host of subatomic particles beyond the normal ones that make up everyday matter. Fermilab explain what the standard model is in this video.
The standard model is basically a table of particles, with a few key sections.
-
6 quarks (and 6 antiquarks) (shown in purple below)
-
6 leptons (which include 3 flavours of neutrino) and corresponding antileptons (shown in green)
-
gauge bosons (force exchange carriers) (in red) and the Higgs Boson (in yellow)
Now, particle physicists have some pretty 'out there' names for stuff that takes some getting used to. I already just talked about the flavour of leptons, despite the fact that no one has tasted one. Names such as charm and strange, top and bottom are just terms given to differentiate one particle from another, it has no bearing on its behaviour!
Now, there a few key terms that are important.
Charge - we are familiar with this concept, though defining what it is can be remarkably tricky. Charge is a fundamental property of matter that causes an interaction due to the electromagnetic force. It is measured in Coulombs (though in particle physics we normally talk about relative charge - relative to a proton/ electron). Particles and antiparticles always have opposite charges.
e.g. an up quark has a relative charge of +⅔. This is the same as ⅔ × 1.6×10ˉ¹⁹ = 1.07 ×10ˉ¹⁹ C.
An antiup quark has a charge of -⅔ (which is the same as -1.07 ×10ˉ¹⁹ C)
If multiple quarks are combined, the total charge is the sum of the individual quark charges (e.g. a proton, uud, has a charge of +⅔ +⅔ -⅓ = +1). Charge is ALWAYS conserved
Mass - again, another fundamental property of matter. All our quarks and leptons are massive (even if some have tiny masses). Some of our bosons are massless, whereas some do have mass. If we look at the table below, our masses are given in MeV/c². This is a common way to present mass in particle physics - it is simply making use of Einstein's E = mc² equation. (note - the c² in the unit to denote that this is a mass - 2 MeV/c² is the mass equivalent of MeV of energy). Particles and antiparticles have the same mass (there is no such thing as negative mass).
e.g. a down quark has a mass of 4.7 MeV/c². To calculate this in kilograms:
4.7 MeV/c² is the mass equivalent of 4.7 MeV of energy. First, We need to use our standard eV: J conversion to convert this to Joules. This becomes 4.7×10⁶ × 1.6×10ˉ¹⁹ = 7.52×10ˉ¹³ J. Lastly, we can use Einstein's E= mc² (or m = E/c²) to work this out as a mass equivalent in kilograms. Dividing by c² gives us a mass for our down quark of 8.36×10ˉ³⁰ kg. The mass of an antidown quark is also 8.36×10ˉ³⁰ kg
If multiple quarks are combined, the total mass is NOT the sum of the constituent quark masses (e.g. a proton, uud, has a greater mass than the sum of the masses of an up, an up and a down quark. This goes back to our idea of binding energy in Section 7.2.
Strangeness - this is a weird property, from which the strange quark is named. The strange quark has a strangeness of -1. The antistrange quark has a strangeness of +1. Everything else has a strangeness of 0. Strangeness is conserved, except through certain weak interactions.
Spin - this is another fundamental property of the particles in the standard model. The IB does not require much understanding of particle spin. It is analogous to the rotation of macroscopic bodies, which have a certain angular momentum. Again, you don't but need to know too much about this, but all quarks and leptons have a spin of +½ - so they are given the collective term 'fermions'.
Particle Families
Now the standard model gives us a list of all the fundamental particles. There are a few key classifications and families that come from the standard model. We saw term fermions previously (that describes our leptons and quarks), as well as the term bosons (which are exchange particles for our fundamental forces).

Quarks
We have 6 quarks (and 6 antiquarks). These are fundamental particles, which means they cannot be broken up further into smaller particles (at least, as far as our standard model goes). You may have heard of quarks as being the building blocks of protons and neutrons, which have a quark structure of Up-Up-Down (written uud) and Up-Down-Down (written udd) respectively. Quarks can be combined in numerous ways to produce a variety of different composite particles called hadrons.
Quarks are bound together in hadrons by the strong nuclear force. It is important to note that I cannot get a individual quark by itself, they are always found within composite particles. For example, if I try and separate the uud quarks within a proton, I put in energy to increase the separation distance. If I put in enough energy to separate these quarks completely, a quark-antiquark pair will pop into existence (through Einstein's E=mc² equation) and create a new set of composite particles - (see pair production in Chapter 12).
A few rules that you need to get to grips with about these particles.
-
All quarks have a baryon number of ⅓ (and antiquarks have an baryon number of -⅓).
-
The top row (up, charm and top) have a charge of +⅓. The bottom row (down, strange and bottom) each have a charge of -⅔. The antiquarks have an opposite charge (e.g. and antibottom has a charge of +⅔).
-
All quarks have a strangeness of 0, other than the strange quark (strangeness = -1) and antistrange (strangeness = +1)
-
All quarks have a lepton number of zero.
Hadrons
Hadrons are family of composite particles that are made up of individual quarks.
The hadron family, is itself made up of sub-families:
-
Baryons are made up of 3 quarks (qqq)
-
Antibaryons are made up of 3 antiquarks (q̄q̄q̄).
-
Mesons are made up of a quark/ antiquark pair (qq̄)
Leptons
Leptons are one of the families of particles:
Video Lessons
Chris Doner | Elemental Particles | Quarks, Leptons and Antiparticles | IB Specific | |||
Physics Online | The Standard Model | Baryons and Mesons | ||||
Science Shorts | Particle Physics | |||||
Study Nova | Particle Physics | Conservation Rules |
Resources
IB Physics | Topic 7 Notes | |||||
IB-Physics.net | Chapter 7 Summary | IB Revision Notes | ||||
Mr. G | 7.3 Teaching Notes | 7.3 Student Notes | ||||
Physics and Maths Tutor | Particles Definitions | Particles Key Points | Particles Detailed Notes | Particles Flashcards | A Level Resources - content slightly different |
Questions
Cambridge University Press | Topic 7: Add Qs | Topic 7: Add Qs MS | Topic 7: MCQs | CUP Website Link | Freely available online | |
Dr French's Eclecticon | Particle Physics | Particle Physics Solutions | Link to Dr French's Site | Extension: Pre-University Material | ||
Grade Gorilla | 7.2 (Particles) MCQ | Topic 7 (Nuclear) End Quiz | Quick IB Specific Mixed MCQs | |||
Isaac Physics | Fundamental Particles and Interactions | |||||
Mr. G | 7.3 Formative Assessment | Topic 7 Summary Qs | IB Specific Questions | |||
Physics and Maths Tutor | MCQ Particles (AQA 2) | MCQ Particles MS (AQA 2) | Particle Classification (AQA 2) | Particle Classification MS (AQA 2) | A-Level Qs: overlapping content | |
Physics and Maths Tutor | Particle Physics (Edexcel 1) | Particle Physics MS (Edexcel 1) | Particle Physics (Edexcel 2) | Particle Physics MS (Edexcel 2) | A-Level Qs: overlapping content | |
Physics and Maths Tutor | Particles, Antiparticles, Photons (AQA 2) | Particles, Antiparticles, Photons MS (AQA 2) | Quarks & Antiquarks (AQA 2) | Quarks & Antiquarks MS (AQA 2) | A-Level Qs: overlapping content |
Fundamental Forces
In Section 2 we looked at different types of forces on a macroscopic scale. However, on an atomic level there exist only 4 fundamental forces of the universe.
These are (In order from strongest to weakest):
-
Strong nuclear force - the force that binds the nucleus together, but only acts over tiny distances
-
Electromagnetism - the force causing attraction and repulsion between charged particles
-
Weak nuclear force - the force that is responsible for beta decay
-
Gravity - the weakest of the lot, the attraction between all objects with mass.

Exchange Particles
Our standard model contains a number of bosons, or force carriers for the various forces (with the exception of gravity, see below). It is an exchange of these bosons that cause these forces.
Taking a simple example of two electrons repelling, we can imagine there is a continuous exchange of photons between the two electrons that causes the electrostatic force of repulsion. Similarly we have our W and Z bosons that are responsible for our weak interaction, and the gluons/ pions which are responsible for the strong nuclear force.
This table summarises some of the key points related to the fundamental forces.
Gravity- Sci Show Video
Gravity is the weakest of the forces (we have explored some of the key ideas of gravitational fields in Section 6.2). The force has an infinite range, and acts between all massive objects. It is by far the weakest of the forces, and it is only with relatively large masses (e.g. astronomical scales) that the size of the force becomes significant. There is a theoretical exchange particle called the 'graviton', though this has not been observed.
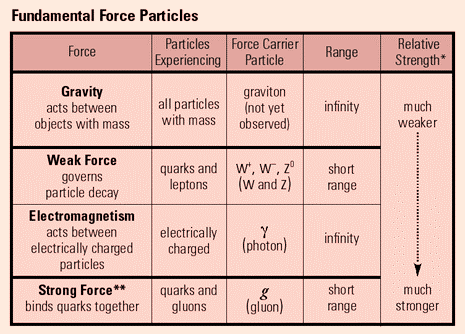
Weak Nuclear Force - Sci Show Video
The weak nuclear force only acts over nuclear distances and is responsible for various type of particle decay. It acts on both quarks and leptons. There are a number of exchange bosons, W+. W- and Z⁰ (with the superscript value representing the charge on the respective boson). In order to understand which boson is acting, Feynman Diagrams should be used.
Electromagnetism - Sci Show Video 1, Video 2
Electromagnetism acts between all charged objects (therefore neutrons and neutrinos do not experience this force). It acts over an infinite distance, with the photon as our exchange particle. It is responsible for our electrostatic and magnetic interactions.
Strong Nuclear Force - Sci Show Video 1, Video 2
The strong nuclear force acts on quarks, and is responsible for binding quarks together. It is an exchange of gluons that binds together our up, up and down quarks in a proton. It is also responsible for holding nuclei together (through the exchange of pions). It is the strongest of the 4 forces, but is short ranged, with a range of approximately 10ˉ¹⁵m. It does not act on leptons (so electrons do not experience the strong force).
Video Lessons
Chris Doner | Exchange Particles | Higgs Boson | IB Specific | |||
Khan Academy | Four Fundamental Forces | |||||
Physics Online | What holds the nucleus together? | |||||
Science Shorts | Particle Physics (Fundamental Forces) | |||||
Study Nova | Fundamental Forces |
Resources
IB Physics | Topic 7 Notes | |||||
IB-Physics.net | Chapter 7 Summary | IB Revision Notes | ||||
Mr. G | 7.3 Teaching Notes | 7.3 Student Notes | ||||
Physics and Maths Tutor | Particles Definitions | Particles Key Points | Particles Detailed Notes | Particles Flashcards | A Level Resources - content slightly different |
Questions
Cambridge University Press | Topic 7: Add Qs | Topic 7: Add Qs MS | Topic 7: MCQs | CUP Website Link | Freely available online | |
Grade Gorilla | 7.2 (Particles) MCQ | Topic 7 (Nuclear) End Quiz | Quick IB Specific Mixed MCQs | |||
Mr. G | 7.3 Formative Assessment | Topic 7 Summary Qs | IB Specific Questions | |||
Physics and Maths Tutor | Particle Interactions (AQA 2) | Particle Interactions MS (AQA 2) | A-Level Qs: overlapping content |
Feynman Diagrams
We've talked about the different types of particles in the standard model so far, and we've talked about the fundamental forces.
Now we've got to grips with that, we can start looking at particle interactions. Feynman Diagrams are a super useful representation of these particle interactions, originally devised by Richard Feynman. Now, Feynman was an American physicist who did a lot of work on nuclear physics (in fact he was involved in the Manhattan Project and the development of the atomic bomb). He later became a professor at Caltech, and presented a series of undergraduate lectures which have since become the gold-standard in Physics teaching. Feynman really is "the physicists' physicist" - articulate, erudite and able to communicate the most complicated scientific ideas in a meaningful and straightforward manner. I present one of my favourite clips below - Feynman talking about ht beauty within a flower:
If you have a bit of time, I recommend learning a little more about Feynman - the BBC have a nice documentary available here.
Anyway, one of his most useful contributions is the development of the Feynman diagram to represent particle interactions, so let's look a bit more closely at these now.
Video Lessons
Chris Doner | Feynman Diagrams | Conservation Laws | IB Specific | |||
Physics Online | Feynman Diagrams | Feynman Diagrams | ||||
Science Shorts | Particle Physics (Feynman Diagrams) | |||||
Study Nova | Feynman Diagrams 1 | Feynman Diagrams 2 |
Resources
IB Physics | Topic 7 Notes | |||||
IB-Physics.net | Chapter 7 Summary | IB Revision Notes | ||||
Mr. G | 7.3 Teaching Notes | 7.3 Student Notes | ||||
Physics and Maths Tutor | Particles Definitions | Particles Key Points | Particles Detailed Notes | Particles Flashcards | A Level Resources - content slightly different |
Questions
Cambridge University Press | Topic 7: Add Qs | Topic 7: Add Qs MS | Topic 7: MCQs | CUP Website Link | Freely available online | |
Dr French's Eclecticon | Particle Physics | Particle Physics Solutions | Link to Dr French's Site | Extension: Pre-University Material | ||
Grade Gorilla | 7.2 (Particles) MCQ | Topic 7 (Nuclear) End Quiz | Quick IB Specific Mixed MCQs | |||
Mr. G | 7.3 Formative Assessment | Topic 7 Summary Qs | IB Specific Questions | |||
Physics and Maths Tutor | Particle Physics (AQA 1) | Particle Physics MS (AQA 1) | Conservation Laws (AQA 2) | Conservation Laws MS (AQA 2) | A-Level Qs: overlapping content |
Additional Resources
IB Questions
A question by question breakdown of the IB papers by year is shown below to allow you to filter questions by topic. Hopefully you have access to many of these papers through your school system. If available, there may be some links to online sources of questions, though please be patient if the links are broken! (DrR: If you do find some broken links, please contact me through the site)
Questions on this topic (Section 7) are shown in dark purple.
Use this grid to practice past IB questions topic by topic. You can see from the colours how similar the question topic breakdown is year by year. The more you can familiarise yourself with the IB question style the better - eventually you will come to spot those tricks and types of questions that reappear each year.







